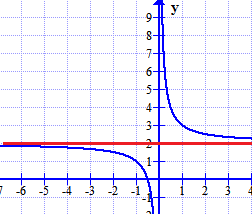
How to find horizontal Asymptotes – CTMaths

How to find horizontal Asymptotes?

A horizontal asymptote is a horizontal line that tells us how the function will behave at every edge of the graph.

A function is an equation of how two things are related to each other. In general, the function tells us how Y is related to X.Usually the functions are often graphed for visualization. The horizontal asymptotes are parallel to X-axis some times it crosses or cuts the graph.

Horizontal asymptotes exist when the numerator and denominator of the function is a polynomial. So we called these functions rational expressions.

Steps for how to find Horizontal Asymptotes

1) Write the given equation in y = form.
2) If there are factors given in the numerator and denominator then multiply them and write it in the form of polynomial.
3) Check the degree of numerator and denominator.
4) If the degrees are same then horizontal asymptote $y=\frac{\left(numerato{r}^{\prime }sleadingcoefficient\right)}{\left(denominato{r}^{\prime }sleadingcoefficient\right)}$

5) If the degree of the denominator greater than the degree of numerator then the horizontal asymptote y = 0 which is nothing but the X-axis.

Examples : 1) Find the horizontal asymptote of the rational function $f\left(x\right)=\frac{3x^2-5x}{x^2-5x+6}$

Solution: First we will write the given function in y form.
$y=f\left(x\right)=\frac{3x^2-5x}{x^2-5x+6}$

Now we will check the degree of numerator and denominator.
Degree of numerator = 2 and the degree of the denominator =2 . Both the degrees are same so horizontal asymptote is given by the formula
$y=\frac{\left(numerato{r}^{\prime }sleadingcoefficient\right)}{\left(denominato{r}^{\prime }sleadingcoefficient\right)}$

Numerator’s leading coefficient = 3 and denominator’s leading coefficient = 1
So the horizontal asymptote is $y=\frac{3}{1}$

2) $f\left(x\right)=\frac{x^3-5}{x-6}$

Solution : First we will write the given function in y form.
$y=f\left(x\right)=\frac{x^3-5}{x-6}$
Now we will check the degree of numerator and denominator.
Degree of numerator = 3 and the degree of the denominator =1 . Both the degrees are different so there is no horizontal asymptote. There is a slant asymptote, that you will learn in the next topic.

3) $f\left(x\right)=\frac{x-8}{x^3-1}$

Solution : First we will write the given function in y form.
$y=f\left(x\right)=\frac{x-8}{x^3-1}$
Now we will check the degree of numerator and denominator.
Degree of numerator = 1 and the degree of the denominator = 3
Since the degree of numerator is less than the degree of denominator.
So the horizontal asymptote is y = 0.

4) Find the horizontal asymptote from the given graph.

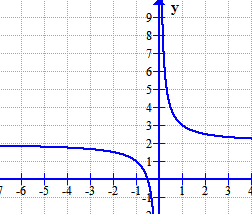
Solution: From the graph, we observe that the horizontal asymptote is at y = 2.